Nick Newland recently wrote an informative article on water ballast for Water Craft magazine (Newland 2015). Following a discussion on the Swallow Yachts Association Forum, this article aims to explain the physics behind the use of water ballast.
Water ballast is… ballast!
A misconception: People use lead or stone for ballast because it is heavier (i.e. denser) than water …so it’s obvious that water won’t work as ballast. Wrong!
 If you were given two closed boxes of equal size and weight with one totally filled with water, and the other with some lead fixed at it’s centre, how would you know which was which? The boxes would seem the same and they would have the same effect when used as ballast in your boat.
If you were given two closed boxes of equal size and weight with one totally filled with water, and the other with some lead fixed at it’s centre, how would you know which was which? The boxes would seem the same and they would have the same effect when used as ballast in your boat.
So water ballast works like any other ballast – end of story! But there are differences. The lead could have been put in a smaller box so it would take up less space in the boat and be positioned lower. With water, the box will take up more space in the hull and probably will be higher in the boat.
On the other hand, if the wind drops and you don’t need ballast, with lead you are stuck with it. With water you can get rid of it and, if you then change your mind you can refill the box from the river or sea. And, you don’t have to take all that weight of water home on the trailer!
This ability to sail a water ballasted boat with tanks either empty or full, depending on the conditions, means it’s worth considering in greater detail the effect ballast has both on boat stability and handling characteristics.
Mass, weight, and buoyancy
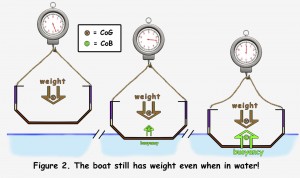
A boat like any other object is made up of various bits of material – wood, GRP, etc. which all added together make up the mass of the boat. The mass of the boat is a physical characteristic which only changes if you add a new gadget, or more ballast, or you break a bit off!
Before putting your boat in the water, if you hang it from a spring balance you would measure its weight. Weight is the force of gravity pulling the boat down. It is proportional to the boat’s mass, and it acts through the centre of that mass, which is called the centre of gravity (CoG). Here on earth, spring balances are calibrated so that the weight is numerically equal to the mass. On the moon your boat would have the same mass as on earth but would weigh less, because gravity is less.
As you lower your boat into the water it starts to be supported by the force of buoyancy. The size of this buoyancy force depends on the amount of water displaced by the boat’s hull. It acts through the centre of buoyancy (CoB) which is the centre of volume of the bit of the boat below the water surface. The boat will settle in the water until it is floating at a level where the buoyancy force exactly balances the weight of the boat. So your spring balance now shows the apparent weight as zero even though the real weight of the boat has not changed, and of course, the boat still has the same mass.
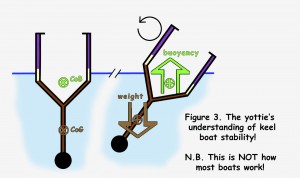
How people think stability works – Deep keeled yachts
Many racing yachts have a very long fin keel with a big bulb of lead at the bottom. For yachts like that the centre of gravity can be below the centre of buoyancy (figure 1). Thus when the yacht heels, the force of gravity and the force of buoyancy act to rotate the boat back towards an upright position.
A longer the keel will give a bigger offset between the CoG and the CoB when the yacht heels, and hence a larger the rotational force bringing the yacht upright. Also a heavier keel will increase both the weight of the yacht and the balancing buoyancy force, again resulting in a larger righting moment.
This “yotties “ view of the world, is NOT how most boats and ships work! However it is how many people tend to think of stability. When they look at a large cruise ship with many decks above the waterline and wonder how it stays upright, they are unconsciously assuming that the CoG must be below the CoB to create stability.
How stability usually works – Most Boats and ships
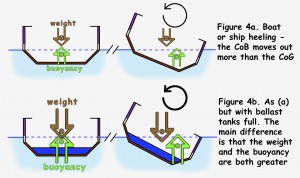
Most boats and ships don’t have a deep keel and the ballast or cargo is carried within the main part of the hull. In this case, the centre of gravity, CoG, is higher than the centre of buoyancy, CoB.
Figure 4a illustrates what happens when the ship or boat heels. Lets assume the view is from astern so the boat heels to starboard. The effect is to move the CoG to starboard and slightly downwards. However the CoB is moved further still in a starboard direction. As a result the weight and the buoyancy form a force couple which tends to rotate the boat back into an upright position.
Figure 4b illustrates the effect of adding a full ballast tank. When the boat is upright it is lower in the water and the CoG is closer to the waterline. As a result, when the boat heels the CoG does not move as far to starboard as when the boat is empty whereas the CoB moves slightly further. This increases the stability compared to the unballasted boat.
However the main effect of filling the ballast tank is to increase the boat’s weight. As discussed above, the boats sinks downwards until the opposing buoyancy force is also increased by the same amount. The two forces tending to rotate the boat upright are therefore, not only spaced further apart, but also much larger. Thus the boat is more stable with a full ballast tank.
That the effect of increased boat weight is important is easy to imagine if you think of trying to tilt a box placed on the ground. If the box is empty it is relatively easy. If the box is full of water it will be much harder to tilt.
Note the increased stability does not require the water ballast to be raised above the water surface, as sometimes believed. As long as the CoB moves out more than the CoG the boat will remain stable, and the heavier the full ballast tank, the more the stability.
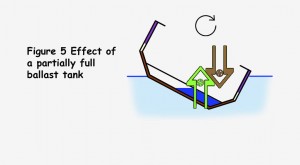
The importance of ensuring that the ballast tank is completely full is illustrated by Figure 5. With a partially full tank, the water, and hence the CoG, moves towards the downward side of the boat. In an extreme case the CoG moves out further than the CoB and boat would become unstable and capsize. This also emphasises that, if you are filling the water ballast tanks following an increase in wind strength, it is desirable that the filling is completed in the shortest time possible. Ballast tanks in Swallow Yachts have internal baffles to increase stability during the process of filling or emptying the tanks.
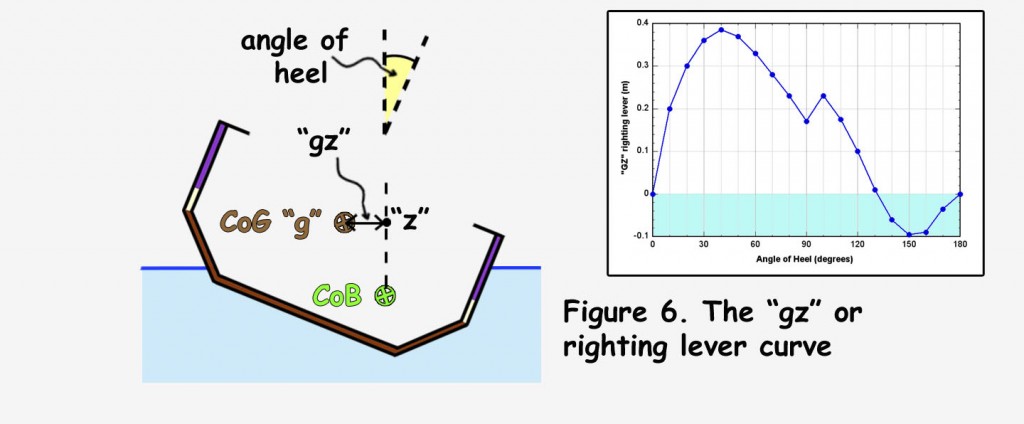
The “gz curve” – righting lever values
To indicate the stability of a boat, yachting magazines publish a “gz curve”. “gz” is simply the horizontal separation of the forces of gravity and buoyancy – what we have just been discussing. It should really be called the righting arm or lever. Figure 6 illustrates how the term “gz” seems to have arisen and shows as an example of a curve (the BC20 with full ballast tanks). For this example the gz value remains positive until about 132° of heel which indicates that the boat would self-right from a knock down condition.
For most boats there is one, characteristic gz curve. But for a water ballasted boat that can be sailed with or without ballast, the large changes in the overall weight and it’s distribution within the boat result in two distinct gz curves. These are shown in figure 7 for four Swallow Boats using data published in Practical Boat Owner (Harding, 2009, 2010, 2011, 2013).
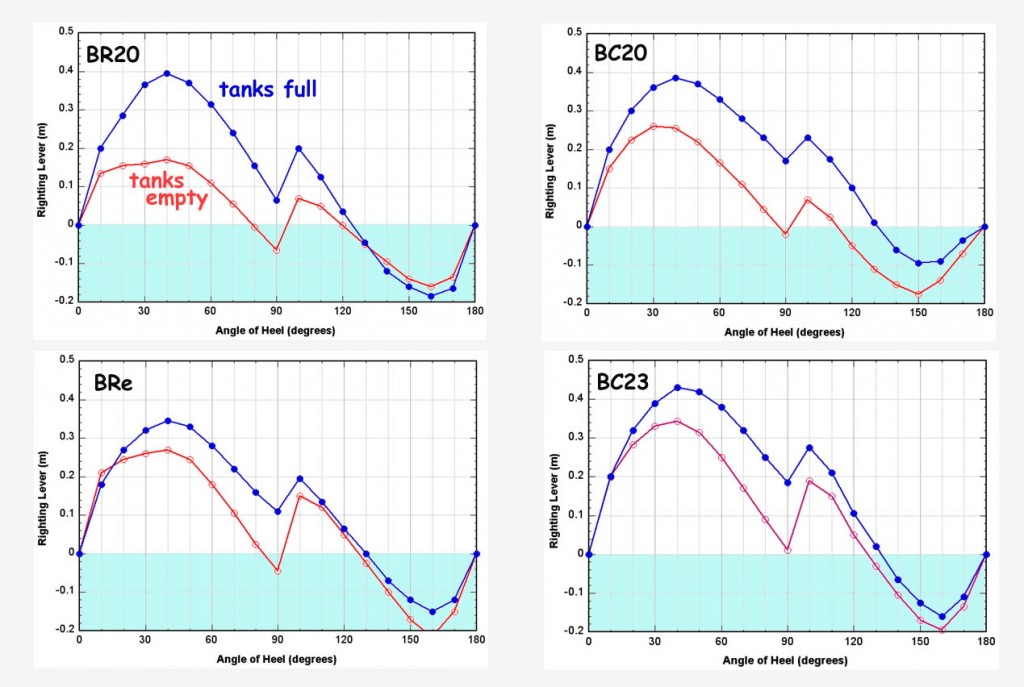
Figure 7 Righting Lever or “gz” curves for various Swallow Boats as published in Practical Boat Owner reviews.
Unfortunately, curves for gz for the ballasted and un-ballasted cases (as in Figure 7) don’t fully represent the effect of ballast on stability because they neglect the change in boat weight. In his article on water ballast, Nick Newland (2015) states that for a Bay Raider, the water ballast increases gz by about 30% but more than doubles the righting moment. ( In fact, for the BR20 Figure 7 suggests that the difference is much more than that. However it is possible that the unballasted curve published in PBO is wrong. It implies that the BR20 is less stable than the BRe which, being more or less a BR20 with a cabin, should be the less stable.)
Comparing the change in stability – the “Righting Moment”
The actual righting force (the “righting moment” ) is given by:
(righting moment, rm) = (righting lever, gz) x (weight of boat)
Unfortunately, righting moment values for different boats are difficult to compare because the boat weights are different. Therefore Figure 8 demonstrates the increase in stability caused by the weight of the water ballast by plotting an “adjusted righting lever” defined by:
(adjusted gz) = ((righting lever gz) x (weight of boat +ballast + equipment))
(weight of bare boat)
Thus, if the boat has no ballast or equipment, the “adjusted gz” is the same as the gz value plotted in Figure 7. The equipment weight (“load” = weight of outboard, cooking gear, battery, etc.) has been added so as not to exaggerate the fractional effect of the water ballast weight by comparing to an empty hull. The nominal values used for each boat are shown in the figure. One should also add in the weight of crew but, since people move around and may even hike out, the crews effect on stability is hard to define and has not been included.
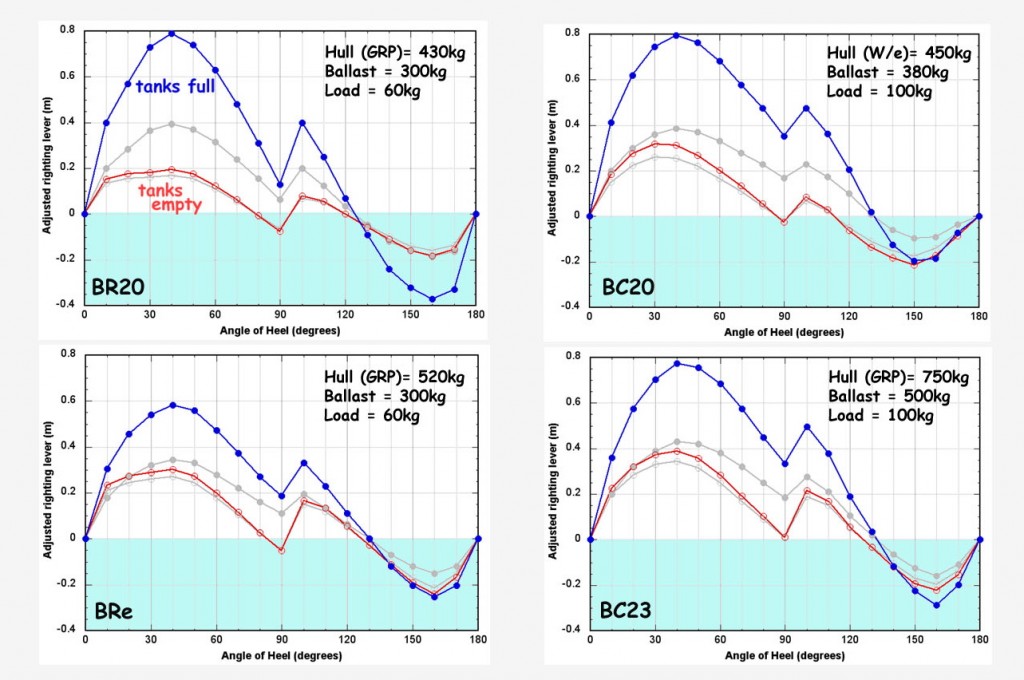
Figure 8 “Adjusted righting lever” values (see text) showing the relative difference in stability between having empty ballast tanks (red) and full tanks (blue). The grey lines are the unadjusted “gz” values as shown in Figure 7.
For the unballasted case the small increased magnitude of the adjusted value (red line) compared to the original gz value (grey) is due to the nominal “load” value assumed. When the ballast tanks are filled with water, there is a small increase in stability due to the change in the righting lever length (upper grey line) but the actual change in stability is much larger (blue line) because of the weight of the ballast.
Stability near capsize
Figures 7 and 8 show that for each of the boats the maximum stability occurs at around 40° of heel. With greater heel the stability decreases with the unballasted curves showing zero or even negative stability when the boat is on its side at 90°. If the position of added equipment such as the outboard were taken into account, the curves suggest that, unballasted, each of these boats would tend to turn turtle. However beyond 90° the curves become positive and for the BR20, BRe, and BC20, the PBO reviews suggest that this is because of immersion of the hollow masts. For the BC23, immersion of the coachroof is suggested. Whatever the cause , this positive stability peak might be enough to keep the boat floating on it’s side rather than turning to 180°.
The situation is much better if the boat is sailed with the water ballast tanks full. In that case all the boats show self-righting ability from a 90° knock down, although the Bay Cruisers, with their smaller cockpits have a greater margin of safety.

Figure 9 The yellow shading indicates the amount of the aft section of a Bay Cruiser 20 hull occupied by the buoyancy tanks needed for self-righting.
Nick Newland (2015) notes that with water ballast this self-righting ability comes at the cost of sacrificing part of the hull space near the gunwale to provide the correct buoyancy distribution. For example the BC20 has large full depth buoyancy tanks at each quarter and across the stern. The hull space lost to tanks for ballast and for buoyancy would seem to be the main disadvantage of using water as ballast.
Dynamic stability
So far the discussion of stability factors has not taken into account the effects of motion.
An oft quoted stability parameter, the “metacentric height” is related to the positions of the centre of gravity and centre of buoyancy, as discussed above. It is of relevance to ships and motor boats since it is related to the period of roll – the time taken to roll one way and back the other, in other words how fast the boats rocking motion is. It is much less relevant for sailing boats because of the aerodynamic forces of the sails and the inertial effect of the mast. More important are factors such as momentum and moment of inertia.
Both the momentum (mass x velocity), and the force needed to accelerate the boat, are proportional to the boat’s mass. Adding water ballast increases the boats mass by exactly the same amount as a similar weight of any other type of ballast. If the ballast tank is full, that extra mass is exists whether the boat is on its trailer or in the water.
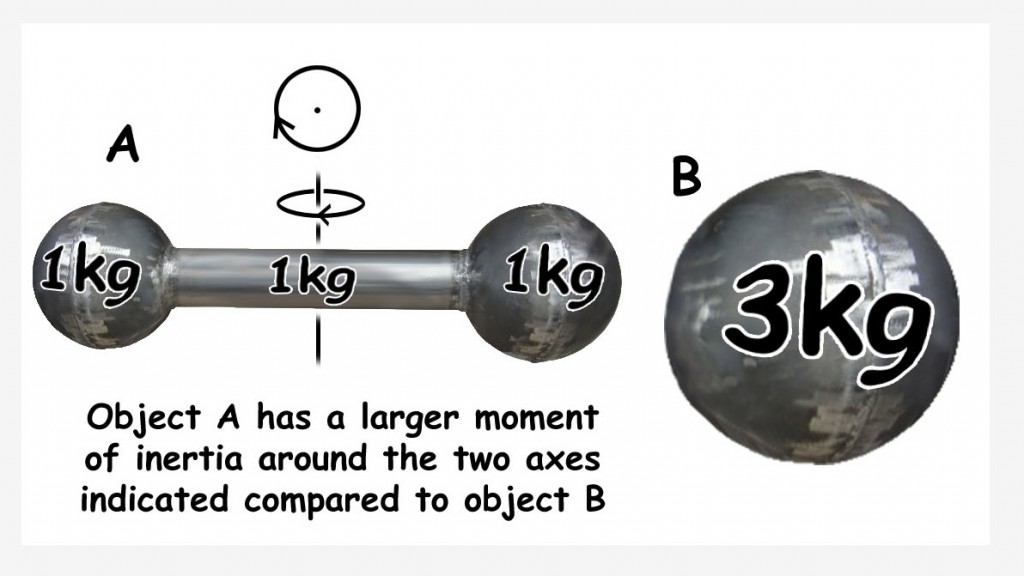
“Moment of inertia” is a measure of how difficult it is to rotate an object around a given axis (Figure 10). Where the water ballast is contained in tanks fore and aft, as in the Bay Cruiser, filling the tanks makes the boat more similar to the dumbbell shaped object. The axes for which moment of inertia is increased are those for yaw and pitch. The roll axis is not significantly affected.
Is the boat faster with ballast tanks full or empty?
Obviously there is no one answer; whether you decide to sail with ballast tanks full of empty will depends on circumstances. If you are out for a day’s sail in your Bay Raider you might have the tanks empty and enjoy planing past another boat which is carrying the equipment needed for a few days cruising. But the cruising owner the security of having a self righting boat might well be the decisive factor in keeping the tanks full.
At least with a water ballasted boat you have the choice and, hopefully the above discussion will help in weighing up the factors. For example, consider beating into a choppy wind sea. Having full tanks will do more than increase stability and allow the boat to sail more upright. The extra momentum (from the increased mass) will mean that the boat is slowed down less by oncoming waves. The increased moment of inertia will make the boat less “twitchy” so it is less deflected from the desired course. You can use the Tiller Tamer and make a cup of coffee!
If you empty the ballast tanks, the boat will be significantly less stable, heeling more and forcing you to spill wind or feather windward. With less mass the boat will be slowed more by slamming into waves. On the other hand, if slowed up by a wave it will then accelerate faster. The lower moment of inertia along the yaw axis will allow the boat to be quicker in responding to the helm. Rather than cut through the waves, you may be able to thread a course between them or (with less inertia to pitching) ride over them. Actively helming the boat dinghy fashion, you might be able to work up higher to windward. However you probably won’t have time to make coffee!
Water ballast gives you the choice and can vary that choice during the course of a day’s sailing.
Water ballast and safety
Finally, it is worth considering the safety factors inherent in a water ballasted boats. First, the ballast tanks create a double skinned hull over much of the boats underwater area. Puncturing a ballast tank will not sink the boat! Second, consider those two crates illustrated in figure 1. If placed in water the wooden crate full of water would float with it’s lid more or less awash. Since the crate containing lead is the same size and weight, it would float in a similar fashion.
Now imagine what will happen if you make a hole in the two crates (figure 11). It won’t make much difference to the crate contain water; it will continue to float more or less at the surface. On the other hand, the crate using lead for ballast will fill with water and sink!
Of course, people like me put heavy things like lead-acid batteries in their boats so even a wooden, water ballasted boat could sink if holed. However it only needs some relatively small sealed buoyancy chambers (as built into Swallow Yachts) to ensure that a water ballasted boat will float even if holed.
(Peter Taylor, February 2015, revised October 2015)
References
Harding, David (2009) A different sort of dayboat (review of BR20), Practical Boat Owner 506, February 2009, 44 – 47.
Harding, David (2010) High-tech tradition (review of BC20), Practical Boat Owner 526, September 2010, 39 – 42.
Harding, David (2011) Technology meets tradition: Baycruiser 23 (review of BC23), Practical Boat Owner 539, September 2011, 40 – 43.
Harding, David (2013) The super-simple trailer-sailer (review of BRe), Practical Boat Owner 556, January 2013, 76 – 79.
Newland, Nick (2015) What’s the Point of Water Ballast?, Water Craft no. 109, Jan/Feb 2015, 30 – 33